原子光子相互作用的拓撲

自從發現量子霍爾效應以來，電子的拓撲相已成為凝聚態物理的一個主要研究領域。利用晶格位置之間的電子跳躍的特定工程，可以預測晶格中的許多拓撲階段。不幸的是，天然晶格(晶體)中相鄰位點之間的距離約為十億分之一米，這使得這種工程非常困難。另一方面，光子晶體具有更大的規模。可見光的光子晶體的晶胞比電子大幾千倍。因此，人們通過挖掘麥克斯韋方程和薛定inger方程之間的相似性而訴諸于拓撲相的光子模擬就不足為奇了，一個名為拓撲光子學的研究領域蓬勃發展。

但是，光子和電子與狗和貓一樣不同。光子本質上是社會性的。他們喜歡聚在一起(這就是為什么我們有激光)。電子彼此討厭。根據費米排斥原則，他們有自己的領地。基于麥克斯韋方程和薛定inger方程之間的模擬的拓撲光子學屬于經典光學，即電子波段拓撲的經典波模擬。很自然地要問，量化光是否嵌入了經典光學解釋之外的新拓撲相位。最近，來自浙江大學的Han Han Cai和Wang Da-Wei揭示了量化光態晶格中的拓撲階段。

光的能量只能存在于離散的包裝中，一個非負整數加上hν的一半，其中h是普朗克常數，而v是光的頻率。整數是該狀態下的光子數，稱為Fock狀態，其中一半是由真空波動引起的。光能的這種離散性是解釋黑體輻射光譜的關鍵(例如，在熔爐中，較高的溫度會將光譜移至彩虹條的藍色側)。光量化也對原子光子產生深遠影響互動。當光場中有n個光子時，被激發原子發射另一個光子的概率與n + 1成正比(請記住，光子是社會性的，他們喜歡新的成員加入)。當光被限制在空腔中時，原子發出的能量可以被重新吸收，這導致原子在激發態和基態之間振蕩，并且振蕩頻率與n + 1的平方根成比例。當原子與光以Fock態疊加時耦合時，即在Jaynes-Cummings(JC)模型中，已觀察到振蕩頻率的這些離散值的頻譜，該模型已成為獲取量子態的標準方法光。

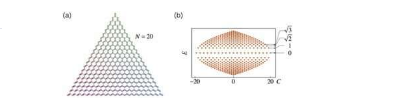
JC模型與拓撲階段無關，但能譜的整數平方根縮放使人聯想到石墨烯中電子的Landau能級，該電子是拓撲階段的搖籃。石墨烯中電子的能帶在布里淵區邊緣的兩個點(稱為狄拉克點)上接觸，服從二維狄拉克方程的電子在其能量和動量之間具有線性關系。當施加磁場時，電子以離散頻率進行回旋加速器運動，其離散頻率與整數的平方根成比例，該整數對應于離散的Landau能級。蔡和王在磁場中建立了三模JC模型和狄拉克電子之間的聯系。