一種使用玻爾茲曼機解決優化問題的新方法

Ising機器是基于物理原理的非傳統計算機架構，以德國物理學家ErnstIsing命名。近年來，人們發現它們是解決組合優化(CO)問題和創建大腦人工模型的特別有前途的工具。

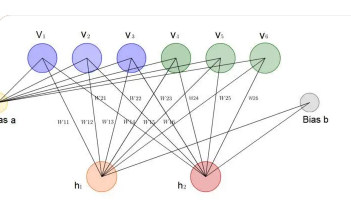
加利福尼亞大學伯克利分校臺積電杰出的EECS教授SayeefSalahuddin小組的一組研究人員最近一直在探索Ising機器在尋找復雜優化問題的解決方案方面的潛力。他們最近發表在NatureElectronics上的論文介紹了一種由許多受限玻爾茲曼機(RBM)組成的新Ising機器，該機器被發現在復雜的組合優化任務上取得了顯著的效果。

“近年來，在Ising機器上進行了大量工作以加速優化問題，我們的工作以此為基礎，”進行這項研究的主要作者SaavanPatel告訴TechXplore。“我們研究的主要目標是展示機器學習和硬件加速如何融入伊辛機器的框架，并以受數字邏輯啟發的方式加速優化問題。”

受限玻爾茲曼機(RBM)是基于人工神經網絡的生成隨機模型。這些模型可以非常擅長捕捉大量輸入數據中的復雜相關性和分布模式。

RBM依賴于二進制激活，繞過了通常對深度學習網絡計算要求最高的直接矩陣向量乘法。在他們的研究中，Patel和他的同事利用模型的這一獨特特性來提高他們的機器解決優化問題的速度。

“我們的算法以一種新的方式使用數字邏輯的基本原理來發揮作用，”帕特爾解釋說。“通常，數字門僅在正向運行，但通過使用概率圖形模型和機器學習，我們已經展示了反向操作它們的方法。利用這一原理，我們以一種可以解決正向的方式設計概率數字電路問題(“這組輸入是一個有效的解決方案嗎?”或“什么是191x223?”)，但由于系統是可逆的，它也可以回答更難的逆問題(“什么是所有輸入產生一個有效的解決方案?”和“什么是A和B使得AxB=42593?”)。

他們開發的機器使Patel和他的同事能夠解決各種不同的優化問題。從本質上講，他們的電路通過最初評估不同的現有解決方案，然后嘗試識別新的解決方案本身來工作。與之前提出的其他解決方案相比，研究人員的平臺將問題映射方法、機器學習和硬件解決方案結合在一起。

“使用我們的數字邏輯方法，我們能夠證明我們可以解決兩種‘困難’問題，”Patel說。“第一個是布爾可滿足性，它構成了組合優化問題的主干，第二個是整數分解問題，它是現代計算機使用的RSA密碼算法的基礎。目標是證明這個工具有效，并且我們證明了我們可以解決比以前提出的方法更大的分解問題。”

在初步評估中，這組研究人員創建的機器取得了非常有希望的結果，解決了復雜的組合優化和整數分解問題。此外，論文中介紹的支持硬件可以比傳統CPU快10000倍地找到問題的解決方案。

將來，像Patel及其同事介紹的那樣的Ising機器可用于更快速、更有效地解決各種復雜的現實世界問題，包括與物流或制造、路由問題和密碼破解相關的問題。在接下來的研究中，研究人員將嘗試升級他們的機器，使其能夠完成越來越大、越來越復雜的優化任務。此外，他們想評估其解決其他類型問題的潛力。

“我們正在設計更大、更高效的FPGA系統以及ASIC，以解決更大的問題，”Patel補充道。“就新的問題領域而言，我們一直在研究路由問題(如旅行商問題)、通信問題(如LDPC編碼)、量子問題(如尋找分子系統的基態)和其他優化問題的映射(“例如，MAX-CUT問題的解決方案)。這些系統有很多新的前沿，我們很高興探索新的空間!我們的目標是始終以更快、更高效的方式解決更難的問題。”