教育資訊：等差數列求和公式及推導方法

目前關于到等差數列求和公式及推導方法這一類的信息是很多小伙伴們都非常關心的，很多人也是經常在搜索關于等差數列求和公式及推導方法方面的信息，那么既然現在大家都想要知道此類的信息，小編就收集了一些相關的信息分享給大家。

等差數列是指從第二項起，每一項與它的前一項的差等于同一個常數的一種數列，常用A、P表示。這個常數叫做等差數列的公差。前n項和公式為：Sn=a1*n+[n*(n-1)*d]/2或Sn=[n*(a1+an)]/2。

等差數列公式

1.定義式

2.通項公式

3.求和公式

4.前n項和公式

等差數列推論

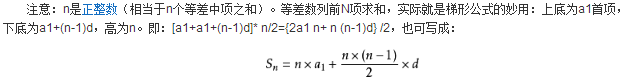
（1）從通項公式可以看出，a(n)是n的一次函數(d≠0)或常數函數(d=0)，(n，an)排在一條直線上，由前n項和公式知，S(n)是n的二次函數(d≠0)或一次函數(d=0，a1≠0)，且常數項為0。

（2）從等差數列的定義、通項公式，前n項和公式還可推出：a(1)+a(n)=a(2)+a(n-1)=a(3)+a(n-2)=…=a(k)+a(n-k+1)，(類似：p(1)+p(n)=p(2)+p(n-1)=p(3)+p(n-2)=。。。=p(k)+p(n-k+1))，k∈{1,2,…,n}。

（3）若m，n，p，q∈N*，且m+n=p+q，則有a(m)+a(n)=a(p)+a(q)，S(2n-1)=(2n-1)*a(n)，S(2n+1)=(2n+1)*a(n+1)，S(k)，S(2k)-S(k)，S(3k)-S(2k)，…，S(n)*k-S(n-1)*k…成等差數列，等等。若m+n=2p，則a(m)+a(n)=2*a(p)。

證明：p(m)+p(n)=b(0)+b(1)*m+b(0)+b(1)*n=2*b(0)+b(1)*(m+n)；p(p)+p(q)=b(0)+b(1)*p+b(0)+b(1)*q=2*b(0)+b(1)*(p+q)；因為m+n=p+q，所以p(m)+p(n)=p(p)+p。

（4）其他推論：

①和=（首項+末項）×項數÷2；

②項數=（末項-首項）÷公差+1；

③首項=2x和÷項數-末項或末項-公差×（項數-1）；

④末項=2x和÷項數-首項；

⑤末項=首項+（項數-1）×公差；

⑥2(前2n項和-前n項和)=前n項和+前3n項和-前2n項和。

數列求和方法

1、公式法

2、錯位相減法

3、倒序相加法

4、分組法

5、裂項相消法

6、數學歸納法

7、通項化歸法

先將通項公式進行化簡，再進行求和。

如：求數列1，1+2，1+2+3，1+2+3+4,……的前n項和。此時先將an求出，再利用分組等方法求和。

8、并項求和法

（常采用先試探后求和的方法）

例：1－2+3－4+5－6+……+（2n-1）-2n

方法一：（并項）

求出奇數項和偶數項的和，再相減。

方法二：

（1－2）+（3－4）+（5－6）+……+[（2n-1）-2n]

方法三：

構造新的數列，可借用等差數列與等比數列的復合。

an=n(-1)^（n+1）

9、求和公式

以上就是等差數列求和公式及推導方法這篇文章的一些介紹，網友如果對等差數列求和公式及推導方法有不同看法與以及，希望共同探討進步。